Introduction
Understanding subset and superset concepts are central to mathematics and set theory, playing an essential role in analyzing relationships between sets and their elements. Through distinguishing subsets from supersets, we gain greater insights into their containment or inclusion within sets.
Recognizing subsets and supersets is key in many fields, including mathematics, computer science, data analysis, logic, and set theory. Understanding this distinction between subsets and supersets is necessary both when studying set theory or applying these concepts in practical applications.Let’s delve deeper into subsets and supersets, exploring their definitions, properties, and any distinctions that set them apart.
Definition of subset
Subset is a mathematical concept used to refer to any collection of elements taken from an initial larger set. If every element in one set A also appears in another set B, A is considered its subset; and set A can then be considered contained within set B.Formally, two sets A and B may be subsets of each other if all elements in A are also elements in B – denoted A B. This definition includes the possibility that both A and B could be considered the same set; in such an instance, A is still considered a subset of itself.Subset comparison enables us to highlight relationships of inclusion and exclusion between sets.
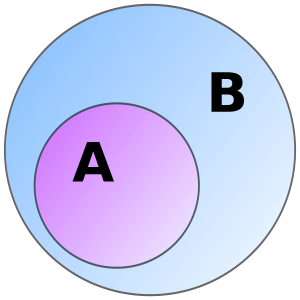
Definition of superset
A superset is a mathematical term that refers to any set that contains all of the elements from another. If, for example, every element from set A exists also within set B (and vice versa), B is then considered to be its superset and encompasses or contains set A.
Formally, two sets A and B can be considered supersets of each other if every element in A is also part of B (this could even apply if A is the same set); B then is considered its own superset in such circumstances.The concept of superset enables us to compare the contents or elements of different sets, highlighting relationships of containment and extension. It creates an umbrella set which contains all elements within an original set as well as potentially new elements that could exist beyond it.

Comparison Table of Subset and Superset
Below is a comparison table highlighting the key differences between subset and superset:
| Subset | Superset |
|---|---|
| A subset is a set containing fewer or equal elements compared to another set. | A superset is a set containing all the elements of another set and potentially additional elements. |
| A ⊆ B denotes that set A is a subset of set B. | B ⊇ A denotes that set B is a superset of set A. |
| A subset includes all the elements of another set. | A superset encompasses or contains all the elements of another set. |
| A subset can be equal to the set it is compared to. | A superset can be equal to the set it contains. |
| Subset relationships: | Superset relationships: |
| Proper subset: A proper subset includes fewer elements than the superset. | Proper superset: A proper superset includes more elements than the subset. |
| Equality of sets: Two sets are equal if they contain the same elements. | Equality of sets: Two sets are equal if they contain the same elements. |
| Subset operations:The union of two subsets combines all their elements without duplication. | Superset operations:The union of two supersets combines all their elements without duplication. |
| Intersection of subsets: The intersection of two subsets includes only the common elements. | Intersection of supersets: The intersection of two supersets includes only the common elements. |
Understanding these differences is essential for accurately describing the relationships between sets, performing set operations, and solving problems involving sets.The table above summarizes the contrasting characteristics of subsets and supersets, providing a clear overview of their distinctions.
Inclusion of elements
Subset: An element from one set can also exist within another. Each subset element also forms part of its superset counterpart; so if set A is considered a subset of set B, that means all its elements can be found within
A superset: encompasses or includes all elements from another set, as well as any additional elements that may exist within it. Each element in a subset forms part of its superset counterpart; and vice versa.When two sets (A and B respectively) are supersets of one another, this indicates that B contains or engulfs all its constituent elements in one collection or set.Subsets of supersets differ by including elements at differing rates; subsets can either contain fewer or equal elements while supersets contain all elements within their subset.
Direction of inclusion
Subset Relationship: Whilst in a subset relationship, inclusion proceeds from subset to superset; any set that contains both elements from A and B can be considered a subset of B. When this occurs, A is considered part of B and considered its subset.
Whilst A may contain elements from more than one superset; every subset contained within each superset counts as part of its superset relationship and vice versa. Subset:Whilst inclusion flows in one direction only in relation to another superset relationship.A subset exists within its superset relationship. When every element from set A is also present within set B then A is considered part of its superset relationship.Willingness to maintain its hierarchy is usually upheld between both sets as members will occupy both sets B’s subset relationship.
Superset Relationship
Superset relationships involve inclusion from one set to another in an upward direction; from superset to subset. A superset encompasses or contains its subset. If every element from set A also exists in set B, B is then considered its superset.Regarding inclusion, subsets can either be included within or encompassed by supersets in terms of direction; when one occurs within another they contain all elements from that subset whereas, on the contrary, supersets include subsets which encompass or contain them entirely.
Size and cardinality
A subset’s cardinality should always be less or equal to that of its superset, for instance when set A is subset of set B then A’s cardinality should always be less or equal than B’s. Subset and superset terms are used interchangeably here.
Cardinality of supersets always exceeds or equals that of their subsets; for example, if set B is a superset of set A then its cardinality must exceed or equal that of A.Subsets tend to be smaller or equal in size compared to their supersets in terms of both cardinality and size; subsets contain fewer elements while supersets may contain all or at least some.A set’s cardinality, or number of elements it contains, represents how large its membership actually is; subsets typically possess smaller or equal cardinalitat than their supersets.
Subset and superset relationships
Subset Relationships: A proper subset is defined as any subset that contains fewer elements than its superset, in other words if every element from set A appears in set B but at least one does not, then A is considered a proper subset of B (and this denoted as A B).
Equality of Sets: Two sets are considered equal if they consist of exactly the same elements. If set A is a subset of set B and vice versa, then A and B are both equal sets, or “A = B.”
Superset Relations: A proper superset refers to any superset which contains more elements than its subset. For example, if every element in set A exists in set B with at least one exception that remains outside B, B is then a proper superset of A and this term should be abbreviated B A.
Equality of Sets: Like subsets, when sets A and B are both supersets of one another they are considered equal sets, often denoted with “A=B.”Subset and superset relationships enable us to compare the containment and inclusion of elements between sets.A properly formed subset/superset relationship indicates strict inclusion; equality among sets indicates they contain exactly identical elements.
Conclusion
Knowledge of subset and superset distinction is vital in a variety of mathematical fields and beyond, and in this content outline we explored their definitions, characteristics, relationships and operations.Subsets refer to collections containing fewer or equal elements compared to another set, defined by inclusion and subset relationships such as proper subsets or equality between sets. Subsets provide for operations like union and intersection.
Supersets encompass or contain all the elements from another set, plus possibly additional ones. Supersets can be classified by their inclusion of elements whose relationships include proper supersets or equality between sets. Supersets also support operations like union and intersection.