Top 10 Differences Between Pattern and Sequence

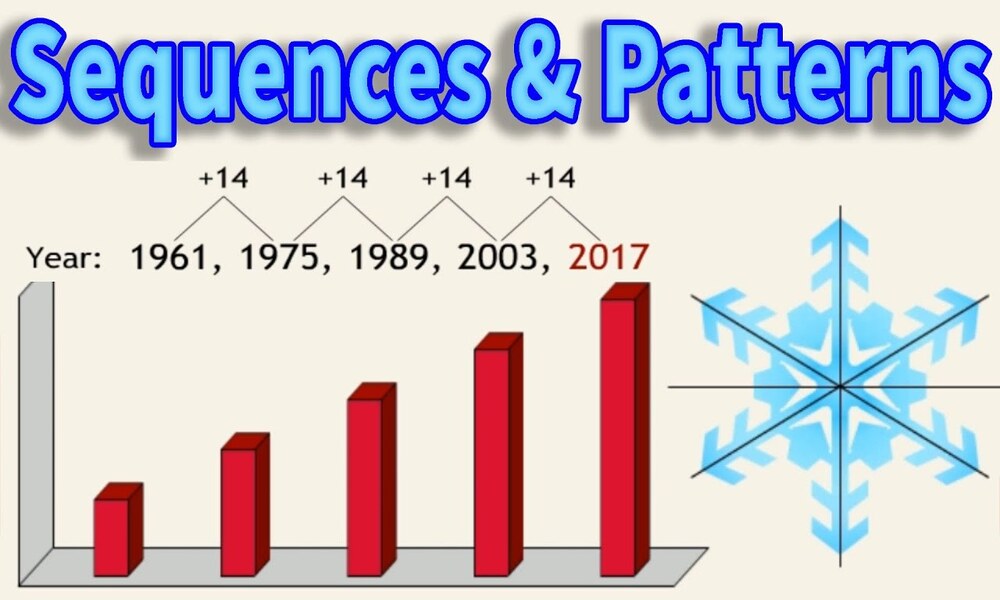
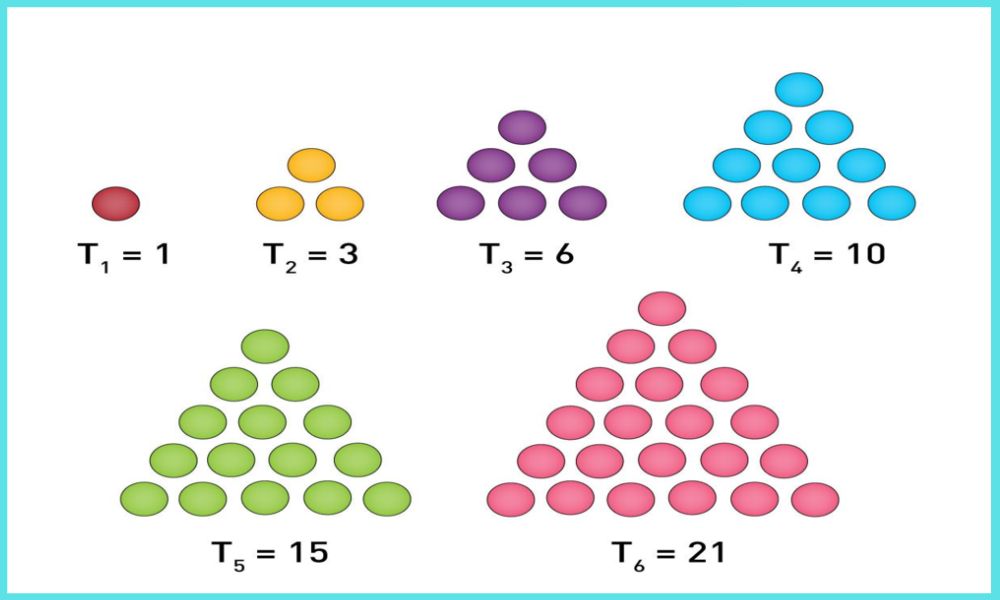
Introduction of Pattern and Sequence

Understanding patterns and sequences is integral to our ability to make sense of information, shaping our perception of reality and comprehending information. Patterns and sequences appear everywhere from nature and mathematics to art and language – even music!While some similarities exist between patterns and sequences, it is essential that they be distinguished so as to fully appreciate their unique properties and applications.

We will investigate why patterns emphasize repetition, regularity, predictability, while sequences place greater emphasis on order progression and logical relationships between elements.Recognizing and comprehending patterns and sequences not only strengthen cognitive skills but can be found useful in mathematics data analysis problem-solving creative endeavors.By exploring the various attributes of patterns and sequences, we can gain a better understanding of their significance in various fields and tap their power. Join us on this voyage as we uncover this world of patterns and sequences.

Definition of patterns

Patterns are repetitive arrangements or sequences of elements that exhibit regularity, predictability and regularity in multiple domains – mathematics, art, nature and human behavior all contain patterns that display these characteristics.Patterns can be observed across disciplines including mathematics, art, nature and human behavior and often include specific shapes, colors, sounds or other elements repeated regularly within them – often repeated recognizable shapes colors sounds or other elements such as music motifs that provide order and structure in our world allowing us to recognize

Recurring relationships or motif easily and comprehend them better – such as straight geometric figures to intricate designs or data sets with complex sequences containing data sets or intricate sequences within them recognizing patterns allows us to make predictions, form expectations, form expectations as well as find meaning within our environments by understanding their patterns within them we gain insight into our world around us and find meaning from what’s out there!

Recognizing patterns allows us to make predictions, form expectations as well as gain meaning from our environments by understanding and making predictions, form expectations as well as making predictions and expectations from what may occur within it thereby helping us form expectations from experiences while discovering meaning in what lies beyond us all in life’s complex sequences within data sets that gives meaning in our lives thereby giving meaning and making predictions while providing us an appreciation of meaning from what lies beyond.

Recognizing them enables us making predictions, form expectations and uncover hidden meaning from within ourselves by making predictions, form expectations recognizing patterns allows us make predictions, form expectations as derive meaning from these in turn recognizing this world around us by making predictions, creating expectations as well as finding meaning out world around us while deriving meaning.

Recognizing patterns allows us predict or making predictions by finding meaningful connections from outside us!. Recognizing /world itself!

Recognizing patterns gives meaning from world around us all around us from. Recognizing them makes predictions to form predictions which gives way; predicts so much better than before using data sets, form expectations as recognizing patterns allows allowing predictions, expectations derived derived meaning from data sets in data set that much better to identify where it all this world around us then deriging meaning from which are given…

Definition of sequences

Sequences are ordered collections or arrangements of elements that follow a predictable sequence or progression. Within such sequences, each element relates to those before or after it in a consistent and predictable fashion – and its order plays an integral role in defining a sequence – this may involve numbers, letters, objects or any other identifiable entities.Sequences may exhibit different kinds of progressions, from arithmetic and geometric progressions to more intricate patterns.

An arithmetic progression features consecutive terms with constant differences, such as 2, 5, 8 11, 14 (an example is 2, 5, 8, 11, 14 with an equal difference of three) while geometric sequences have common ratios between consecutive terms – such as 2, 6, 18, 54 162 which also has three terms in it as examples of such progressions.Sequences can be found across disciplines such as mathematics, computer science, music and literature. Sequences provide an effective means of organizing information, recognizing trends and solving problems more efficiently.Recognizing and understanding sequences helps identify patterns as well as uncover underlying relationships within series of elements.

Comparison Table of Pattern and Sequence

Below is a comparison table highlighting the key differences between patterns and sequences:

Aspect	Pattern	Sequence
Definition	Arrangement exhibiting repetition, regularity, and predictability.	Ordered set of elements following a specific pattern or progression.
Emphasis	Repetition, regularity, and predictability.	Order, progression, and logical relationships.
Components	Composed of individual elements forming a recognizable arrangement.	Composed of a series of elements following a specific order.
Characteristics	Repetition of specific elements or motifs. <br> – Regular and organized arrangement. <br> – Predictable and recognizable pattern.	Ordered arrangement of elements. <br> – Logical progression or relationship between elements. <br> – Incrementation or decrementation in value or other attributes.
Examples	Geometric shapes, color combinations, musical motifs.	Numeric sequences, alphabetical order, Fibonacci sequence.

This table provides a concise overview of the distinctions between patterns and sequences. Patterns focus on repetition, regularity, and predictability, whereas sequences emphasize order, progression, and logical relationships between elements. Understanding these differences is crucial for recognizing and interpreting patterns and sequences in various contexts.

Strategies for analyzing patterns

When it comes to analyzing patterns, there are various strategies you can employ in order to gain a better understanding of their structure, rules, and relationships.

Below are some effective techniques for examining patterns:

Identify Elements: Take a close look at the pattern and identify its individual components or elements – these could include shapes, numbers, colors, words or any other recurring units within it.

Search for repetitions: Determine whether there are elements or motifs which repeat throughout the pattern and note their frequency and placement.

Examine the Arrangement and Order: Analyze how elements are organized within their patterns, seeking patterns in their positioning, orientation or sequence of elements.

Determine Pattern Type: Classify your pattern into one or more types based on its characteristics – geometric, numeric, visual or language patterns? Understanding its type may provide insights into its rules governing its development.

Recognize the Pattern Rule: Strive to uncover the rule or relationship that governs a pattern. Look for consistent changes, transformations or operations applied to elements as the pattern progresses – for numeric patterns this might include operations such as arithmetic operations, geometric progressions or functional relationships.

Test the pattern rule: Use the identified rule to predict or generate subsequent elements in a pattern and see if these predictions match up with actual elements of that pattern for accuracy testing of its rule.

Investigate Variations: Play around with variations to the pattern by altering or expanding its elements or rules, as this will reveal different facets or possibilities within it.

Visual Aids: Make use of visual representations such as diagrams, charts or graphs to aid pattern recognition and analysis. Visualization can often reveal hidden patterns which might otherwise go unnoticed.

Comparing with existing patterns: To gain additional insights or deeper understanding, compare the pattern you are studying with those found elsewhere such as mathematics, nature, art or language. Doing this may provide additional connections that deepen your knowledge.

Make use of others: Discuss or collaborate on the pattern with others to gain multiple perspectives and insights. A different viewpoint could reveal hidden patterns or interpretations that you had overlooked.

Consistent practice of pattern analysis will sharpen your recognition skills and strengthen your ability to decipher complex patterns. The more patterns you explore and analyze, the better at you’ll become at understanding their underlying structures and rules.

Strategies for analyzing sequences

Analyzing sequences involves closely inspecting their order and progression in order to discover patterns or rules governing their arrangement.

Here are some strategies that will help you effectively analyze sequences:

Establish the Sequence Type: Determine what kind of sequence it is you are dealing with; common types are arithmetic sequences, geometric sequences and recursive sequences. Understanding its type provides a starting point for analysis.

Examine Differences or Ratios: For arithmetic sequences, look for constant differences between consecutive terms; while for geometric sequences, look for constant ratios between consecutive terms. Analyzing these differences or ratios can reveal patterns and assist your analysis process.

Calculate Terms: Use the existing terms of a sequence to calculate missing terms and identify relationships or formulas which generate it, while at the same time expanding it and verifying its accuracy.

Look for Patterns in Differents or Ratios: Keep an eye out for patterns in either differences (for arithmetic sequences) or ratios (for geometric sequences) between consecutive terms in an arithmetic or geometric sequence and note any regularities or trends that emerge.

Explore Recursive Formulas: Recursive sequences are defined in terms of previous terms in the sequence. Identify the formula which generates it and understand how each term relates to previous ones.

Search for an explicit formula: Some sequences possess explicit formulas that allow any term to be computed directly without using past terms as reference points. When possible, search for such an explicit formula which represents your sequence.

Consider transformations: Try altering the sequence by performing transformations like adding or subtracting constants, multiplying by factors, or applying functions to individual terms. Doing this may reveal hidden patterns or establish relationships among multiple sequences.

Compare to Well-Known Sequences: Compare a given sequence with well-known sequences from mathematics or other domains, to gain insights or analogies that may aid analysis. Look for similarities or connections between your sequence and other similar patterns.

Use visual representations: Plot the sequence on a graph or create a table to visualize its pattern, which can help detect trends, periodicity or irregularities that might not otherwise be easily visible. This strategy may reveal hidden trends or irregularities.

Test and Validate: Employ the identified patterns, formulas, or rules to predict and validate subsequent terms in the sequence. Verify if your predictions match with either actual terms provided or additional ones you calculate yourself.

Implementing these strategies can give you a deeper understanding of the patterns and rules underlying sequences. Be systematic when conducting your analyses; document findings as you go, and try different approaches for dealing with sequence analysis effectively.

Extending patterns and sequences

Extending patterns and sequences involves projecting or creating additional terms based on an identified pattern or rule.

Below are a few strategies for expanding patterns and sequences:

Apply the Found Pattern Rule: Make use of the pattern rule or formula you have identified to add more terms to a sequence. Apply it consistently across each term to generate additional elements in iterations.

Verifying Extension: Once extended terms have been added to a pattern, verify them against it to make sure they adhere accurately to established rules and are consistent with existing patterns. This step helps validate its reliability as well as verify if an extension matches up well with existing patterns.

Explore alternative rules or variations: Explore variations on a pattern rule to generate different sequences. Modify it by adding or subtracting constants, multiplying and dividing by factors or including other operations – this strategy allows you to create diverse sequences while maintaining their fundamental structure.

Recursive Extensions: When dealing with recursive sequences, use the recursive formula to generate subsequent terms. Each term is calculated based on previous ones and thus defines an recursive relationship within the sequence itself. Continue recursion until expanding your sequence is achieved.

Explore Different Starting Points: Experiment with various initial terms or starting points within your pattern or sequence. By shifting this starting point, you can observe how the sequence develops over time and reveal new branches or variations within it.

Recognize patterns within patterns: Patterns can contain sub-patterns or nested structures that need to be explored more deeply and intimately. Aiming at analyzing repeating units within larger patterns and expanding individual motifs within them provides for an in-depth examination of them all. This approach offers more sophisticated exploration.

Analyse periodicity: If a pattern exhibits periodic behavior, determine the length of its period to extend its sequence and repeating within that timeframe can create new terms in its cycle.

Generalize the pattern: Take its underlying principles or concepts, and apply them in other contexts or problem-solving scenarios, broadening its reach beyond its original sequence. This generalization helps broaden and deepen its purpose.

Test Your Extensions: Review any extended terms against given or known data if available, comparing their extended sequence with any observed patterns to ensure they follow established rules and relationships.

Analyzing real-life applications: Explore real-life scenarios or applications where your pattern or sequence could appear. Apply it in these contexts and observe its evolution over time and across contexts.

By employing these strategies, you can extend patterns and sequences beyond their given terms, explore variations, discover nested structures, and apply the patterns to various scenarios. Testing and validating extensions will further deepen your understanding of a pattern’s applicability.