Best 5 Difference Between Prime Number and Prime Factors

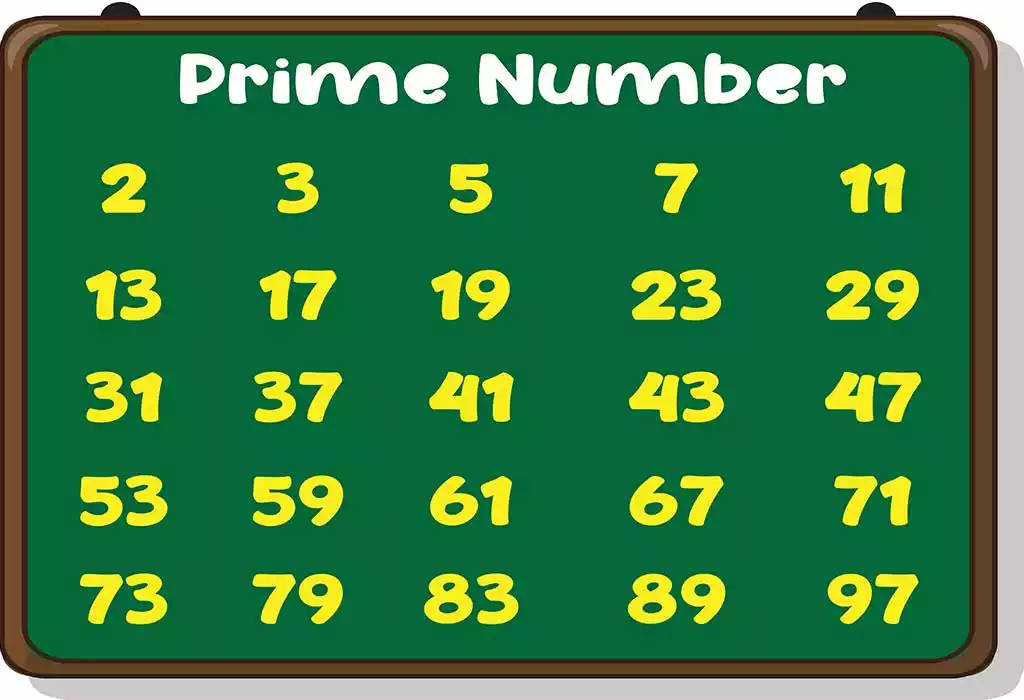
Prime Number

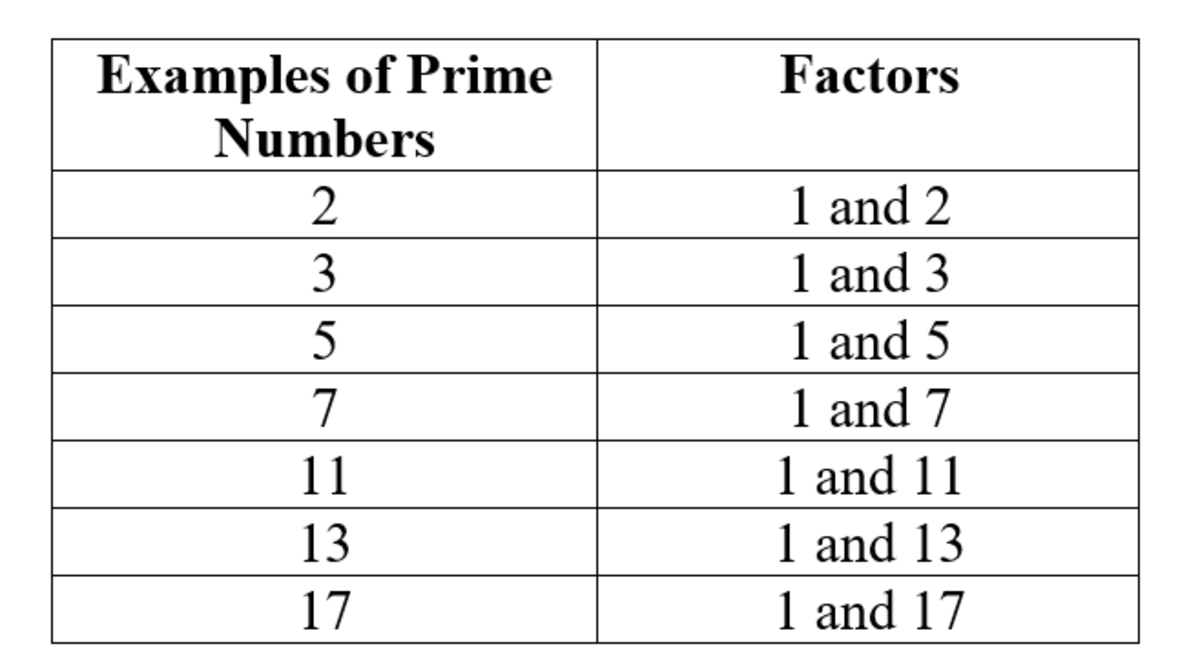
Prim numbers can be described as a specific kind of whole number that is greater than 1, which can only be divided by one and itself. Also, the prime number has precisely two positive divisors. For instance, 2,3 5, 7, 11 13, 17, 19 23, 29, and 31 are all prime numbers.

Prime numbers have a number of significant properties, such as:

• Prim numbers always have positive integers larger than 1.
• Every positive integer has its own prime factorization. This means that it is able to be written as a product from prime numbers in a distinct manner.
• The prime number distribution is not uniform This means that there isn’t a formula to determine the prime number that will be next.

Prime numbers are utilized in a myriad of mathematical applications, such as the field of cryptography, number theory in addition to computer science. They also are used throughout the day, for instance in finding the dimensions of a rectangular object that has a specific size or to find the most common divisor of two numbers.

Prime Factors

Prime factors are those that make up the parts of a number that include a prime number. Also, a prime factor is a prime number that is able to divide the given number but does not leave an unfinished. For instance, the prime factors of 24, are and 3. 2 3 x 2 equals 24.

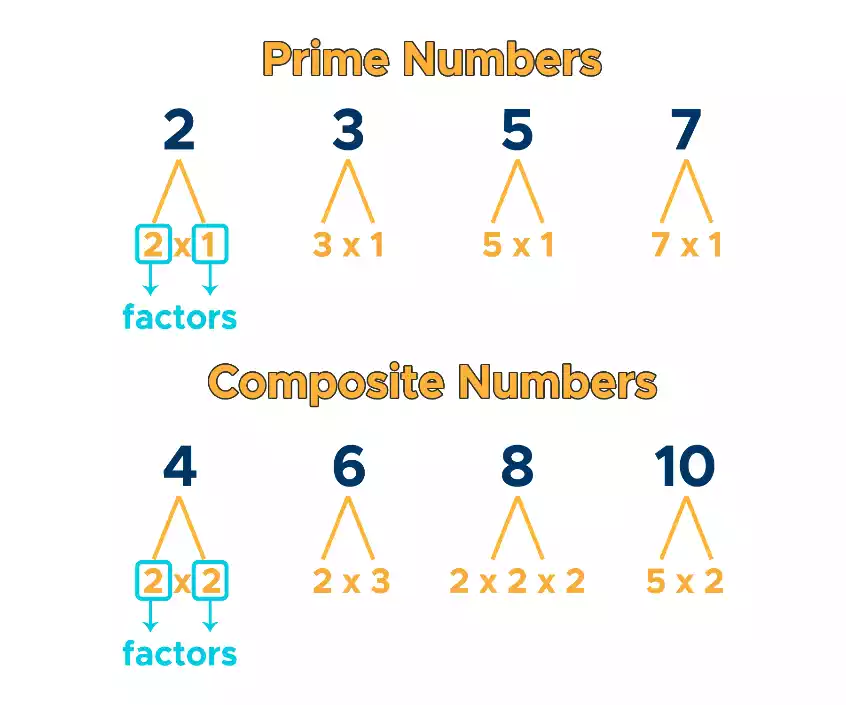
Every positive integer is unique in its prime factorization. This means that it is able to be written as the product of prime numbers, in a distinct manner. For instance, the prime factorization for 60 is 2 3 x 2 x 5. This means that 60 could be defined as a combination of prime factors 2,3 and 5, in a distinctive manner.

Finding the factors that make up a prime given number is helpful in many math-related applications, like simplifying fractions, determining the largest common divisor for two numbers, and in resolving problems related to the field of number theory. In the field of computer science, prime factorization is employed as a cryptographic method to encode or decode data.

Comparison Table of Prime Number and Prime Factors

Here’s a comparative tables of Prime Numbers and Prime Factors:

Criteria	Prime Numbers	Prime Factors
Definition	Numbers that can only be divisible by one and themselves	Factors of a particular number that are prime numbers
Examples	2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37	The main factors of 24 is 2, 3, and 2.
Properties	Prim numbers always have positive integers larger than 1	Every positive number has a distinct prime factorization
Identification	It can be determined by determining whether it has exactly two positive divisors	You can find the answer by dividing the number primary numbers, until the number ceases to be dispersible by the prime number
Relationship	Prim factors comprise the fundamental blocks of prime numbers.	Prime numbers are the result of its prime elements
Example Problem	Determine if 23 can be a prime number.	Find the most important elements of 60
Solution	23 is comprised of exactly two positive divisors, 1, and 23. Therefore, it is a prime number.	divide 60 times 2 for 30, multiply 30 by 2 to get 15 Then, divide 15 by 3 to get 5. The most important factors are 2, 3, and 5 2,, and 5.

Note The table below isn’t complete and contains only a few of the major factors for comparison of prime number and prime factor.

How to recognize prime numbers

There are a variety of methods to find prime numbers:

1. Test Division Method: Determine whether the number n is evenly divided by any integer that is between two and the square root. If not, then it can be considered a prime. To determine, for example, whether 17 is prime we must multiply it with all numbers in between the two numbers and then by its square root (which is roughly 4.12). We can see that 17 cannot be divided by 2, 3 or 4, which means it is a prime.
2. Sieve of Eratosthenes: Create an inventory of all numbers between 2 and the number n. Remove every multiple from 2. (except the 2 itself) and then go to the next number unmarked (which will be 3) and then cross out all three multiples (except the 3 itself). Repeat this procedure for all numbers that are unmarked up until the square root of. The remaining numbers that are not marked have all been prime.
3.  To determine: for example, all primes from 1 to 30 we begin by separating every multiple of two, except for 2 itself and then all multiples of 3, except those for the number 3 by itself and then the entire multiple of five with the exception the 5 themselves. The remaining numbers that are not marked are 7, 11, 13 17, 19, 23 29, and these are all prime numbers.
4. Fermat’s Little Theorem: If p is a prime digit and an is an integer that is not more than p that is, then a to power of p-1 less 1. is divisible by. This could be used to examination of prime numbers but it’s not practical for large numbers.
5. Miller: Rabin Primality Test is a probabilistic method that is utilized to determine if an arbitrary number could be a composite number or a prime one. This is an approach based upon the concept that a number is a reliable indicator of the compositeness of the number.
   

   How to find prime factors

   To determine the prime elements of a number take these steps:

   1. Then, divide the total by the most prime number which divides it evenly. For instance, if the total is 24 you can divide it by 2. 2. is the most compact prime number that evenly divides 24. That gives you 12.
   2. Divide the quotient you obtained at step one by the smallest prime number which divides it evenly. For instance, if the number of quotients is 12, then divide it by two more times since 2, which is the most compact prime digit which divides 12 evenly. That gives you six.
   3. Continue to divide the quotient with the smallest prime number until you have reached the quotient of one. Prime factors in your original number are the prime numbers you used to divide the number.

   For instance, in order to determine the most important factor of sixty, perform these steps:

   1. Divide 60 by 2. This gives you 30.
   2. Divide the 30th by 2 times This gives you 15.
   3. Multiply 15 with 3, giving 5.
   4. The five quotient is a prime figure, therefore the prime factors of 60 are 2, 3 and 5.

   The order of the prime factors isn’t important because any rearrangement of the prime elements will result in the same final product.

   Conclusion

   Prime numbers as well as prime factors are crucial mathematic concepts with a variety of applications across a variety of areas. Prime numbers are positive integer that is greater than 1 with only two positive divisors: 1 and. Prime factors are number that divides a number without leaving a residuum.

   Every positive integer has its own prime factorization. This means that it is able to be expressed as a result of prime factorization in a distinct manner. The recognition between prime and non-prime factors can be important in many computational and mathematical applications including numbers theory, cryptography, and computer science.