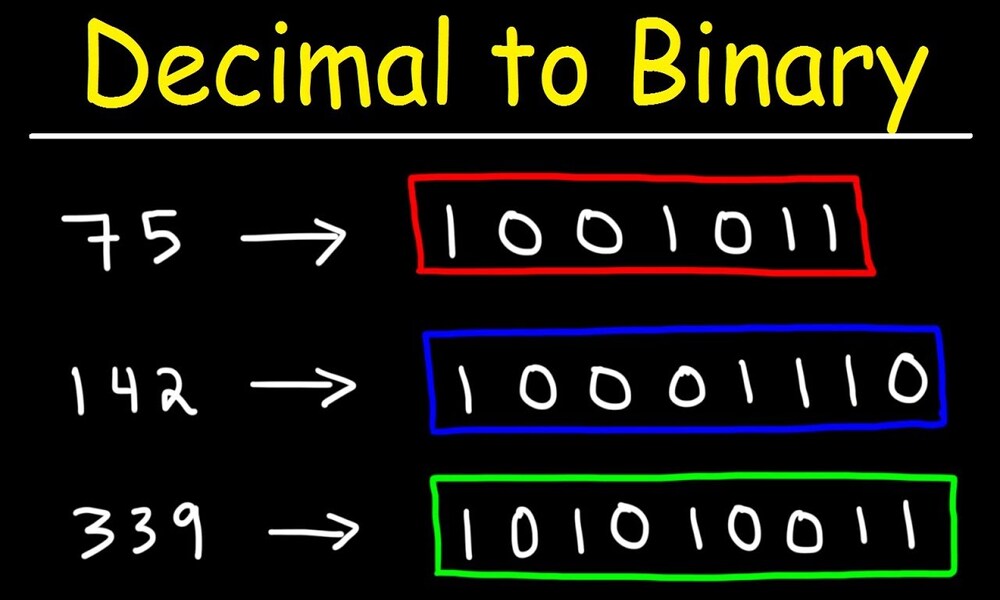
What is Binary and Decimal?
Binary:
Binary is a system of numbers which utilizes just two numbers (1 and 0) to represent numbers as well as perform mathematical operations. Each individual number in binary is known as a bit; their location in any particular number determines their value – for instance the rightmost part represents 20 (1) while 2(n-1) represents 2 most crucial bits within any number (known as MSB/LSB respectively).
Binary is used widely in digital electronics and computing to represent data as well as perform calculations. Furthermore, binary serves an integral function in cryptography, telecom and other fields where precise storage and transmission require precision and efficiency.Therefore it’s crucial for everyone involved in digital technology to comprehend binary as it forms the core foundation of how computers and other digital devices function.
Decimal:
Decimal is a numerical system comprised of ten digits from 0-9 used to represent numbers as well as carry out mathematical operations. Decimals use decimals only, where every number has an associated value according to where it sits in a decimal number’s representation; wherein 100 (1 is represented by rightmost digit and 10(n-1) by last one (the latter value being determined by number of digits making up that particular decimal).
Decimal is one of the most Frequently Employed number systems used in daily life, often for Counting, Measuring, and calculations. Its usage spans Multiple Disciplines including science, Finance Engineering science as well as other Requiring Precise Calculations such as Science.
Decimals form the Cornerstone of Mathematics as they act as Foundation for many Mathematical systems such as Algebraic Equations and more complex Arithmetical operations such as Trigonometric Functions.
Comparison Table of Binary and Decimal
Here is a table that compares the use that compares Binary as well as Decimal
| Aspect | Binary | Decimal |
|---|---|---|
| The number of Digits | 2 (0, 1) | 10 (0-9) |
| Base | 2 | 10 |
| Positional Value | Each digit represents the power of 2. | Each digit represents 10 times the power. |
| A Variety of Numbers | Smaller range of numbers, which can be numbers that can be as high as 2n-1 | Greater range, can represent numbers that can be as high as 10n-1 |
| Operations | Basic operations in arithmetic are carried out by using binary | Basic operations in arithmetic are carried out by using decimal |
| Applications | Digital electronics, and network | It is used in everyday life finance engineering, science, and finance |
| Conversion | Conversion from decimal to binary is necessary | Conversion from decimal to other systems is necessary |
| Benefits | Effective in digital processing and storage | Easy to comprehend and use in most situations. |
| Negatives | It is difficult to read and comprehend for humans. | Not suitable for certain types of digital processing |
Both decimal and binary each have their advantages and drawbacks, and the selection of which to utilize will depend on the particular needs of the job at the moment.
While binary is a good choice for specific types that require digital manipulation, decimal is more widely known and easy to use in the majority of situations.
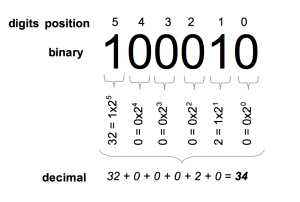
Binary number system
Binary number systems enlist just two numbers, zero and one, to represent numbers and perform mathematical operations. Within the binary number system is its mathematical counterpart called bit theory: each number in this system can be classified by location – the rightmost part known as the most important bit (LSB), is 20 (1) while 2(n-1) represents two more important bits in any number (MSB).
The binary is widely utilized in digital electronics and computing for representing data and performing calculations, while computers store all their information as binary numbers; computers may show “A” as 010000011, where each bit represents an aspect of what each letter stands for.
Basic operations, including multiplication, subtraction, addition, and division can all be accomplished using binary calculation; however, the result differs significantly from traditional decimal calculations. When adding binary numbers together the result could either be 0, 1, or 10 (carryover), unlike in decimal addition.
Converting between decimal and binary is possible and often necessary in digital information processing. To convert binary values to decimals, multiply each bit’s positional value before adding up their totals; when translating decimals back to binary format divide by 2 then store remainders until your quotient equals zero in an Excel sheet.
Overall, binary numbers system is an indispensable concept in digital technology as it forms the core of how computers and other digital devices function.
Decimal Number System
A decimal system of numbers employs the ten digits 0-9 as its basic unit to represent numbers numerically as well as perform mathematical operations. Each number in a decimal system corresponds with one of its positions within that particular number’s value hierarchy – where 100 represents 100-1 while 10(n-1) represents total amount of digits present within it.
Decimal is one of the most frequently employed number systems, used for counting, measuring, and making calculations in everyday life. It has numerous applications within finance, engineering science, and other areas where accurate calculations must take place.
Basic operations of multiplication, subtraction, addition, and division can all be accomplished using decimal math. Decimal addition results range from 0-9; borrowing can also occur up to nine places away in subtraction calculations.
Converting decimals to other numbers such as binary, hexadecimal, or the octal system can also be achieved easily and is frequently needed when working with various formats of data.
When changing from decimals to another number system requires multiplying each decimal with its base value until your quotient equals zero; conversely to convert numbers from other systems back into decimals multiply each number with its respective position and add up the results before multiplying again by 1.
Decimal number systems are an indispensable concept to those working in numbers and mathematics; it forms the backbone for both traditional arithmetic as well as many other mathematical systems.
Future Directions for Number Systems Development
Numerology has played an essential part in shaping civilizations over time, adapting as society evolved. Technology will likely further advance this evolution by creating new number systems as well as improving existing ones.
Here are a few potential future directions in creating systems of numbers:
As quantum computing becomes more advanced, new number systems that accurately represent quantum-like states and operations may emerge that better support complex computations than traditional numbering schemes.
Such number systems could even incorporate various mathematical theories instead of traditional numeration systems for greater efficiency when handling quantum calculations. Nonlinear Number Systems Nonlinear number systems such as the p-adic number system have long been studied but have yet to become widely utilized in practical settings such as encryption, cryptography, error-correcting codes or even physics.
With improved technology and new software being released, it could become more prevalent across fields like encryption, cryptography, and error-correcting codes; cryptology; error-correcting codes, or even physics.
Multidimensional Number Systems Current number systems primarily operate using representations in one dimension of numbers; however, as science continues to explore higher levels of physics as well as other fields, multidimensional number systems could emerge to reflect them.
Simple number systems The traditional numbers system may be challenging for children who are young or have learning disabilities to master and use effectively, however as we create new educational tools and techniques more intuitive number systems may emerge which make mathematics simpler to comprehend and apply for all.
As such, creating and improving new numbering systems will become an area of investigation and advancement over the coming years. They could potentially be applied across numerous areas.
Conclusion
Binary and decimal numbers are essential concepts in math and computing. Composed of only two digits: zero and one respectively, they find widespread application in digital electronics and computing. Decimal is an extensive numerical system comprised of 10 digits from 0-9 that is widely utilized.
While basic operations, including subtraction, addition, and division may all take place using either system, their methods differ considerably. As technology progresses, new number systems could emerge across various fields. Examples may include quantum systems, nonlinear multidimensional ones, and intuitive ones – among many other possibilities. As our society changes over time, new numbers systems or modifications of existing ones could emerge to meet ever-evolving societal requirements.