Difference Between Integration and Differentiation

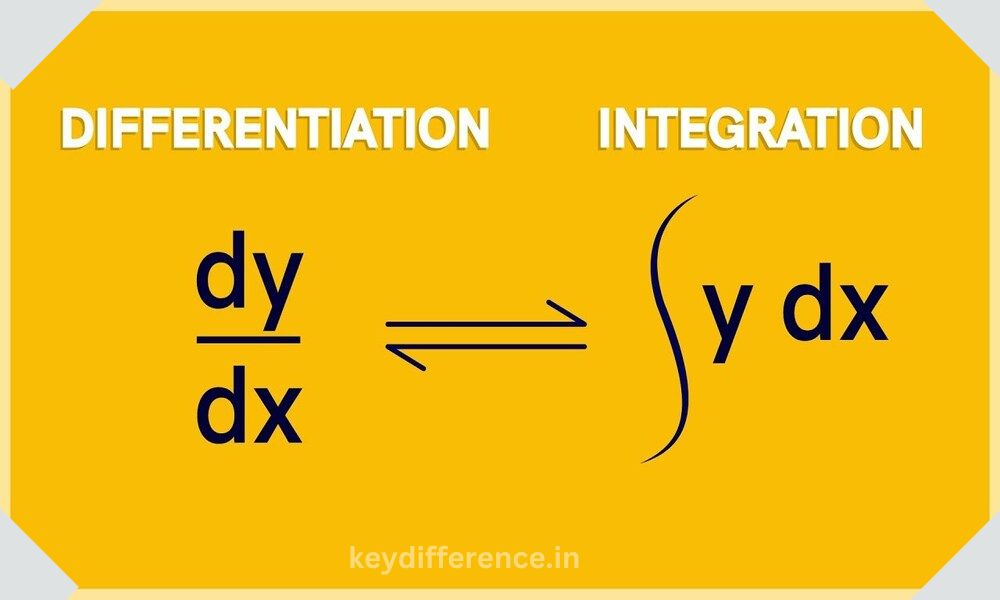
Definition of Differentiation and Integration

Integration and differentiation are two fundamental concepts in calculus that are closely related but serve distinct purposes.

Differentiation: Differentiation, as Used here, refers to an Application of Mathematics which Examines rates of change Between Variables in relation to one Another. Derivation refers to the process of finding out where in an equation its derivative lies along a given tangent line at any particular location in an equation – used mainly to understand function behavior as well as tackle engineering, physics and economic issues that arise within these equations.

Basic rules of differentiation encompass rules such as the power rule, product rule and quotient rules as well as chain rule.

The power rule States that, for a Function where its value Remains Constant over time (f(x) = xn), its Derivative can be Described by: “f'(x) equals nx(n-1).” Rule of Product states that, when both Functions f(x) and g(x) share an Identical Function and one function (g(x) in this Instance) exists as well, then their Derivative can be Calculated using “(f(x)g(x)”) which equals (f(x)g'(x) + g(x)f'(x). The Quotient Rule states that, when two functions f(x) and g(x) differ significantly, then their derivative can be determined using this equation: [f(x)/g(x))” = “g(x)f'(x)(x) – [g(x)g'(x)]/g(x). Finally, Chain Rule provides guidance in how to calculate composite functions’ derivatives which involve two or more functions combining.

Example applications of differentiation include finding the derivative of an expression such as: f(x) = x2 + 3x + 2, as well as finding out that its incline at certain locations on its formula such as: sin(x). Differentiation can also help solve complex problems like finding the speed or speed of moving objects.

Differentiation can be applied across diverse fields including engineering, physics, economics and biology. When used within these domains it helps analyse motion in physics; within economics demand and supply curves; while biology employs differentiation for studying development and growth processes of living organisms.

Integrity is a mathematical concept focused on finding the area of curves. This process reverses differentiation by finding their antiderivatives – functions with derivatives inverse to that of their original function.

Integration: Integration involves four basic rules. They are substitution, the power rule through substitution, integration via parts trigonometric integrals and integration by parts. If a given function f(x) = xn (where n is greater than or equal to 1) then its derivative will be F(x) = (x(n+1 )/(n+1) + C – for an integral constant such as C; otherwise integration by substitution and parts trigonometric integrals require trigonometric operations instead.

Integration may involve finding the integral of a function like f(x)=x2 + 3x + 2, or the area under an arc like sin(x) between variables x = 0 and pi, among many other applications such as finding total distance traveled with respect to velocity functions of moving objects.

Integration can be used to solve issues in many fields including economics, engineering, physics and even probability. Integration can help calculate energy and work in physics; engineers use integration to estimate impacts from structures; in economics it can calculate profit from manufacturing operations while in probability it determines density for continuous random variables.

Comparative Table for Integration and Differentiation

Here is a table of comparison of integration and distinction:

Integration	Differentiation
Definition: Finding the derivative of a function to calculate the area under the curve.	Definition: determining the derivative of a function in order to determine the change rate of a particular quantity in relation to another.
Differentiation reversed.	Opposition of integration.
Fundamental rules include an integration rule that is power-based, as well as integration via substitution, integration with parts, and trigonometric integrations.	The basic rules are the rule of power, the product rule and quotient rules as well as the chain rule.
Conceptually, it measures the accumulation of changes over a certain period.	Conceptually determines the change rate at a specific point on the curve.
Finds the area that is under the curve.	Determines the slope of a Tangent line.
A process that is global and involves adding innumerable small portions of an arc.	Local process that involves the analysis of a tiny portion of the curve.
The degree of the polynomial function by one.	Reduces the complexity of the polynomial function by one.
Non-linear operator.	Linear operator.
A multi-step process which may need different approaches for various types of tasks.	A single-step process that utilizes an amalgamation of the most basic guidelines.
Applications in engineering, physics economics, probabilities, and many other areas.	Applications in engineering, physics and economics, biology, and many more areas.

In short the integration and differentiation concepts are two of the fundamental concepts in calculus, with numerous applications across a variety of areas.

Integration is concerned with determining the area of an arc and determining the change that accumulates over a certain period of time while differentiation focuses on understanding the slopes of a line as well as measuring the change rate at a specific point on the curve.

Although they are two different methods, both are essential for solving issues in engineering, science economics, as well as other areas.

Derivation (d) means finding a function’s derivative; for example: f(x) = x2 + 3x + 2, with its derivative being 2x+3 and so forth.
Trigonometric Derivative functions should be identified using Trigonometry such as sin(x) = sin(x), cos(x) or sin(x). To find these functions you need a Trigonometric table and Calculators or online Services available Online that allow for Trigonometric graphing and Calculations.
Determination of exponential derivative functions such as f(x) = ex and f'(x) = ex is known as derivative analysis.
Finding the Logarithmic Derivation of an Exponential function such as f(x) Requires using the Formula: Ln(x), where F'(x) = 1/x
Finding functions with equations similar to these requires finding two functions, with values as f(x) = x2 sin(x), or 2x sin(x) + cos(x).

Calculating an Equation that derives the ratio Between two Functions such as f(x), Which Equals (x2 + 1)/(x + 1): F'(x) = (2x(x- 1) – (x2 + 1))/((x – 1)2).

Figuring Out the Base of a Composite Formula Such as F(x) = (2x + 1)3:
These examples demonstrate some fundamental rules of differentiation such as power rule products rule, rule of quotients rule and chain rule, as well as their applications to determine an angle between two tangent lines and solve various physics-related problems that come up in engineering, economics or any other area of study.

 Examples of integration

F(x) = x2+3x +. (x2/3 + 3×3) is known as an integral function and C is its constant.

Find the area under f(x), where x = 0, 1, 2, etc and pi: mes SIN(X), where Sin is sin(X). From pi to zero this becomes (-cos(pi), (-cos(0) and so forth until 2.

Integral integration used to resolve a physical problem and determine how work was accomplished by applying constant force F over distance d (Work = Fdx + Work done on distance D).
Integrating to locate particle systems’ mass centers:

Integrate (1/M) Dmx = (1/C), where C represents particle location and M represents total system mass.

Integrating to calculate total profit through industrial procedures: Total Profit = (R(x) + C(x))DX where R(x) is revenue function and C(x) represents costs while x is product quantity.

These examples demonstrate how integration could be utilized to determine an antiderivative of an equation or calculate an area under a curve, in addition to solving questions in engineering, physics economics and other areas of science and math.

They also illustrate its application in situations like locating particles at their center of mass within a system and calculating earnings generated by processes.

Applications of Differentiation

Differentiation can be employed across many fields and applications. Here are just a few examples:

Differentiation is an approach used in Physics to measure velocity and speed during motion. A derivative of position in relation to time reveals velocity; an acceleration relationship then determines acceleration.

Differentiation in Economics serves to identify marginal revenue, cost and profit formulas. A derivative function relating to cost can yield marginal cost estimates while producting revenue functions relates to quantities will yield estimated margin revenue figures; any gap between them represents profit.

Engineering: Differentiation is used to calculate curvature and slope of curves used when designing structures such as tunnels and bridges, such as by using slope derivative functions that calculate curvatures of curves. A slope derivative function calculates curvatures.

Biology: Differencing can help explain the development and decline of populations. By deriving a population function in relation to time, differentiation reveals changes in its dynamics that allow analysis.

Differentiation can help reveal the rate at which chemical reactions take place. By measuring how quickly products or reactants accumulate relative to time, we can gain an accurate idea of their rate of oxidation or reduction.

Computer Science: Differentiation is utilized by machine learning and AI algorithms such as gradient descent. Gradient analysis uses function gradients to detect which direction offers steepest decline and may help optimize cost functions by providing information for cost function optimisation.

Differentiation has many applications across many fields and disciplines. As one of the cornerstones of calculus, differentiation also finds widespread usage across engineering, science economics and other areas of study.

Applications of integration

Here Are A Few Examples interieur Integration is an expansive term with numerous uses in multiple areas. Here are just a few examples:

Integration can be used to determine velocity, displacement and acceleration for subjects in motion. An integral calculation comparing relative speeds provides displacement information while integral calculation using relative acceleration gives velocity details.

Engineering Integrals are widely utilized by engineers for measuring the amount of work accomplished over distance by force across an interval. An integral of distance provides information regarding work completed.

Integral analysis in economics allows one to accurately calculate costs, revenues and profit functions. When used on marginal revenues, an integral can generate the revenue function; otherwise it provides cost functions while its difference yields profits as profits.

Biology Integration can be used to examine how resources in biological systems deplete and accumulate over time, providing an approximate value of these assets in relation to time. Changing rates give insight into this resource’s total worth over time.

Probability and statistics combine to calculate both the likelihood of events within probability theory, as well as to evaluate random variables’ potential values using statistics.
Integration Signal Processing: Integration can be used to map out where signals exist within either frequency or time domains and extract valuable data from them such as video, audio and biological signals.
Integration has many applications in diverse areas. Integration serves a key purpose in calculus and has wide-reaching use in engineering, science economics as well as other domains.

Conclusion

Integration and differentiation are among the core operations in calculus, with numerous applications across many fields of inquiry. Differentiation involves discovering a function’s derivative relative to one or more variables while integration involves finding its antiderivative.

Differentiation may be used for finding slopes or changes in rates while integration identifies areas or total amounts that must accumulate; both processes are utilized across engineering, physics, biology and economic disciplines alike – understanding differentiation and integration is vital in order to effectively tackle complex research questions across fields like economics or biology among many more disciplines!